En estadística, existen diversas pruebas para analizar la relación entre variables. Las variables nominales son las que permiten relaciones de igualdad y desigualdad, como por ejemplo el género.
En este artículo conoceremos una de las pruebas para analizar la independencia entre variables nominales o superiores: la prueba chi-cuadrado, a través del contraste de hipótesis (pruebas de bondad de ajuste).
- Artículo relacionado: "Análisis de Varianza (ANOVA): qué es y cómo se usa en estadística"
¿Qué es la prueba de chi-cuadrado?
La prueba chi-cuadrado, también llamada Ji cuadrado (Χ2), se encuentra dentro de las pruebas pertenecientes a la estadística descriptiva, concretamente la estadística descriptiva aplicada al estudio de dos variables. Por su parte, la estadística descriptiva se centra en extraer información sobre la muestra. En cambio, la estadística inferencial extrae información sobre la población.
El nombre de la prueba es propio de la distribución Chi-cuadrado de la probabilidad en la que se basa. Esta prueba fue desarrollada en el año 1900 por Karl Pearson.
La prueba chi-cuadrado es una de las más conocidas y utilizadas para analizar variables nominales o cualitativas, es decir, para determinar la existencia o no de independencia entre dos variables. Que dos variables sean independientes significa que no tienen relación, y que por lo tanto una no depende de la otra, ni viceversa.
Así, con el estudio de la independencia, se origina también un método para verificar si las frecuencias observadas en cada categoría son compatibles con la independencia entre ambas variables.
¿Cómo se obtiene la independencia entre variables?
Para evaluar la independencia entre las variables, se calculan los valores que indicarían la independencia absoluta, lo que se denomina “frecuencias esperadas”, comparándolos con las frecuencias de la muestra.
Como es habitual, la hipótesis nula (H0) indica que ambas variables son independientes, mientras que la hipótesis alternativa (H1) indica que las variables tienen algún grado de asociación o relación.
Correlación entre variables
Así, como otras pruebas para el mismo fin, la prueba chi-cuadrado se utiliza para ver el sentido de la correlación entre dos variables nominales o de un nivel superior (por ejemplo, la podemos aplicar si queremos conocer si existe relación entre el sexo [ser hombre o mujer] y la presencia de ansiedad [sí o no]).
Para determinar este tipo de relaciones, existe una tabla de frecuencias a consultar (también para otras pruebas como por ejemplo el coeficiente Q de Yule).
Si las frecuencias empíricas y las frecuencias teóricas o esperadas coinciden, entonces no hay relación entre las variables, es decir, éstas son independientes. En cambio, si coinciden, no son independientes (existe relación entre las variables, por ejemplo entre X e Y).
Consideraciones
La prueba chi-cuadrado, a diferencia de otras pruebas, no establece restricciones sobre el número de modalidades por variables, y no es necesario que el número de filas y el número de columnas de las tablas coincida.
Sin embargo, sí es necesario que se aplique a estudios basados en muestras independientes, y cuando todos los valores esperados sean mayores de 5. Como ya hemos mencionado, los valores esperados son aquellos que indican la independencia absoluta entre ambas variables.
Además, para utilizar la prueba chi-cuadrado, el nivel de medida debe ser nominal o superior. No tiene un límite superior, es decir, no nos permite conocer la intensidad de la correlación. Dicho de otro modo, el chi-cuadrado toma valores entre 0 e infinito.
Por otro lado, si aumenta la muestra, aumenta el valor de chi-cuadrado, pero debemos ser cautos en su interpretación, porque eso no significa que haya más correlación.
Distribución chi-cuadrado
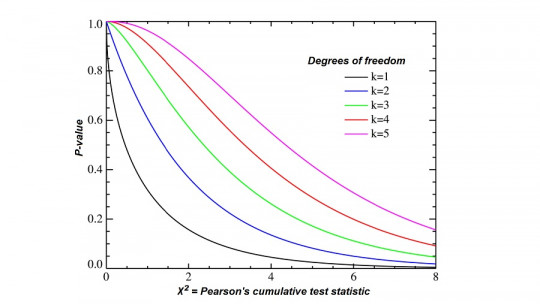
La prueba chi-cuadrado utiliza una aproximación a la distribución chi cuadrado para evaluar la probabilidad de una discrepancia igual o mayor que la que exista entre los datos y las frecuencias esperadas según la hipótesis nula.
La exactitud de dicha evaluación dependerá de que los valores esperados no sean muy pequeños, y en menor medida de que el contraste entre ellos no sea muy elevado.
Corrección de Yates
La corrección de Yates es una fórmula matemática que se aplica con tablas 2x2 y con una frecuencia teórica pequeña (menos de 10), para corregir los posibles errores de la prueba chi-cuadrado.
Generalmente, se aplica la corrección de Yates o también “corrección por continuidad” cuando una variable discreta se aproxima a una distribución continua.
Contraste de hipótesis
Además, la prueba chi-cuadrado pertenece a las llamadas pruebas de bondad de ajuste o contrastes, que tienen el objetivo de decidir si puede aceptarse la hipótesis de que una muestra dada procede de una población con una distribución de probabilidad totalmente especificada en la hipótesis nula.
Los contrastes se basan en la comparación de las frecuencias observadas (frecuencias empíricas) en la muestra con aquellas que cabría esperar (frecuencias teóricas o esperadas) si la hipótesis nula fuera cierta. Así, la hipótesis nula se rechaza si existe una diferencia significativa entre las frecuencias observadas y las esperadas.
Funcionamiento
Como hemos visto, la prueba chi-cuadrado se utiliza con datos pertenecientes a una escala nominal o superior. A partir de chi-cuadrado, se establece una hipótesis nula que postula una distribución de probabilidad especificada como el modelo matemático de la población que ha generado la muestra.
Una vez tenemos la hipótesis, debemos realizar el contraste, y para ello disponemos de los datos en una tabla de frecuencias. Se indica la frecuencia absoluta observada o empírica para cada valor o intervalo de valores. Entonces, suponiendo que la hipótesis nula es cierta, para cada valor o intervalo de valores se calcula la frecuencia absoluta que cabría esperar o frecuencia esperada.
Interpretación
El estadístico chi-cuadrado tomará un valor igual a 0 si existe concordancia perfecta entre las frecuencias observadas y las esperadas; por contra, el estadístico tomará un valor grande si existe una gran discrepancia entre estas frecuencias, y consecuentemente se deberá rechazar la hipótesis nula.
Referencias bibliográficas:
- Lubin, P. Macià, A. Rubio de Lerma, P. (2005). Psicología matemática I y II. Madrid: UNED.
- Pardo, A. San Martín, R. (2006). Análisis de datos en psicología II. Madrid: Pirámide.
