Hoy en día es habitual que tengamos que trabajar con grandes cantidades de datos, independientemente de si nos dedicamos a la investigación o a otros sectores.
Para ello es necesario ser capaz de operar con ellos, y a menudo comparar y ordenar datos entre sí. Y en este sentido, pueden sernos de utilidad utilizar medidas de posición a través de las cuales separar los valores totales de aquello medido en varias partes para localizar en qué posición se encuentra uno de ellos. Uno de los más conocidos y útiles es el percentil. Pero... ¿qué es un percentil?, ¿cómo calcular percentiles? Veámoslo a lo largo de este artículo.
- Artículo relacionado: "Psicometría: ¿qué es y de qué se encarga?"
¿Qué es un percentil?
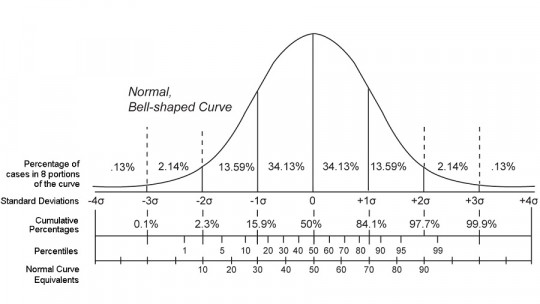
Se conoce como percentil o centil a una de las más frecuentes medidas de posición de datos, la cual implica la división del total de aquello que se está midiendo en 99 partes para obtener un total de 100 partes iguales. De esta manera, la totalidad de aquello que se está midiendo está representado en algún lugar de estas 99 partes, y el o los datos concretos ocuparán una posición entre dichas partes. Se trata de un tipo de cuantil o fractil, valores que permiten separar datos en grupos con el mismo número de valores.
Dicho de otro modo, los percentiles son cada una de las posiciones que ocupan unos datos cuando se divide la totalidad de los datos existentes en cien partes, marcando la posición que deja por debajo de sí a un tanto por ciento determinado de la población correspondiente con el valor del percentil per se (es decir por ejemplo el percentil 1 es el que deja por debajo al 1%). Asimismo deja por encima de sí otro tanto por ciento relevante.
Conceptos vinculados
El concepto de percentil se encuentra íntimamente ligado al de porcentaje, pero sin embargo se trata de conceptos diferentes: mientras que el porcentaje es un cálculo matemática que nos permite visualizar una cantidad determinada como fracción entre cien partes iguales, el percentil nos indica la posición que tiene que ocupar un dato para dejar por debajo al tanto por ciento correspondiente.
Asimismo, el percentil es un valor que también se asocia con otras medidas de posición, como los cuartiles o los deciles. La diferencia radica en el número de divisiones y la escala sobre la que observamos en qué posición están nuestros datos. De hecho, los cuartiles y deciles se corresponden con diferentes percentiles, dado que no dejan de ser la posición que ocupan unos datos en diferentes escalas. Los diferentes cuartiles corresponden con los percentiles 25, 50 y 75, mientras que los deciles se corresponden con los percentiles 10, 20, 30, 40, 50, 60, 70 y 90.
¿Para qué sirven?
Saber qué es y cómo calcular un percentil, aunque no lo parezca, puede ser de gran utilidad en múltiples ámbitos. El percentil no deja de ser un valor que nos permite realizar comparaciones y ordenaciones entre sujetos, casos o grado de existencia de un factor o variable en un conjunto, algo que nos permite trabajar a un nivel muy fácilmente comprensible con conjuntos de datos más o menos amplios y establecer una posición para los que estamos obteniendo.
Esto, a nivel práctico, puede ayudarnos a determinar por ejemplo si un atributo o variable se encuentra dentro de valores normales o si se encuentran por debajo o por encima de la media. Ejemplos de ello los encontramos en que resultan de ayuda para determinar si una función neuropsicológica se encuentra o no alterada, si los niveles de inteligencia se encuentran dentro de la normalidad si comparamos los resultados de un sujeto con los de su población de referencia o si un niño tiene un peso y altura cercano o lejano a la media para su edad.
- Quizás te interese: "Tipos de test psicológicos: sus funciones y características"
Calcular percentiles: ¿cómo hacerlo?
Calcular percentiles es un proceso relativamente sencillo, bastando con tener todos los datos representados del mismo modo y llevar a cabo un cálculo simple. Sin embargo, para ello se requiere no solo tener un dato concreto, sino tener claro qué tipo de puntuación se va a ordenar y con respecto a qué y quiénes se va a realizar la comparación.
De hecho, si empleamos diferentes instrumentos de evaluación veremos con frecuencia que existen tablas de referencia para valorar entre qué valores oscila un percentil determinado para poder asociar los datos obtenidos experimentalmente con dicho percentil. Estas se llevan a cabo con mediciones exhaustivas con una muestra representativa de la población de referencia.
Cuando tenemos que calcular un percentil es necesario tener en cuenta en primer lugar si estamos trabajando con datos ordenados o no ordenados. Cuando los datos no están agrupados u ordenados, la posición en la que se halla el percentil podrá calcularse dividiendo el producto del percentil por el número de elementos de la muestra de la que partimos entre cien. La fórmula sería P=(k*n)/100.
Cuando estamos ante un conjunto de datos ordenado, podemos seguir la fórmula Px=Lri+((kn/100 - Fa)/f)(Ac). Así, bastará con sumar el límite inferior de la clase donde está el percentil a producto entre la amplitud de la clase y el cociente entre la resta de la posición menos la frecuencia acumulada anterior y la frecuencia total.
Asimismo, encontrar un percentil determinado de un conjunto de datos (por ejemplo buscar el percentil 25 de un conjunto o base de datos) únicamente requiere dividir el número de valores menores que el que tenemos por en número total de valores y multiplicar este resultado por cien.
