Cuando se investiga en psicología, se emplea frecuentemente la estadística descriptiva, que ofrece modos de presentar y evaluar las características principales de los datos a través de tablas, gráficos y medidas resúmenes.
En este artículo conoceremos el coeficiente de correlación de Pearson, una medida propia de la estadística descriptiva. Se trata de una medida lineal entre dos variables aleatorias cuantitativas, que nos permite conocer la intensidad y dirección de la relación entre ellas.
- Artículo relacionado: "Alfa de Cronbach (α): qué es y cómo se usa en estadística"
La estadística descriptiva
El coeficiente de correlación de Pearson es un tipo de coeficiente empleado en estadística descriptiva. Concretamente, se utiliza en la estadística descriptiva aplicada al estudio de dos variables.
Por su parte, la estadística descriptiva (también llamada análisis exploratorio de datos) agrupa un conjunto de técnicas matemáticas diseñadas para obtener, organizar, presentar y describir un conjunto de datos, con el propósito de facilitar su uso. En general, utiliza tablas, medidas numéricas o gráficas como apoyo.
Coeficiente de correlación de Pearson: ¿para qué sirve?
El coeficiente de correlación de Pearson se utiliza para estudiar la relación (o correlación) entre dos variables aleatorias cuantitativas (escala mínima de intervalo); por ejemplo, la relación entre el peso y la altura.
Es una medida que nos da información acerca de la intensidad y la dirección de la relación. En otras palabras, se trata de un índice que mide el grado de covariación entre distintas variables relacionadas linealmente.
Debemos tener clara la diferencia entre relación, correlación o covariación entre dos variables (= variación conjunta) y causalidad (también llamada pronóstico, predicción o regresión), ya que son conceptos diferentes.
- Quizás te interese: "Prueba de chi-cuadrado (χ²): qué es y cómo se usa en estadística"
¿Cómo se interpreta?
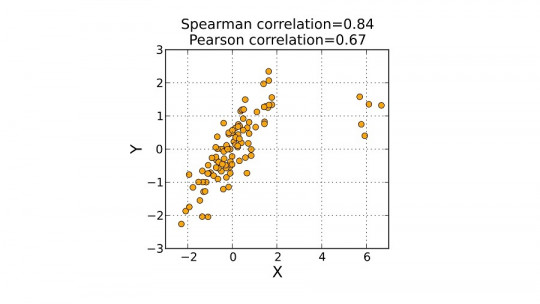
El coeficiente de correlación de Pearson comprende valores entre el -1 y el +1. Así, dependiendo de su valor, tendrá un significado u otro.
Si el coeficiente de correlación de Pearson es igual a 1 o a -1, podemos considerar que la correlación que existe entre las variables estudiadas es perfecta.
Si el coeficiente es mayor que 0, la correlación es positiva (“A más, más, y a menos menos). En cambio, si es menor que 0 (negativo), la correlación es negativa (“A más, menos, y a menos, más). Finalmente, si el coeficiente es igual a 0, sólo podemos afirmar que no hay relación lineal entre las variables, pero puede haber algún otro tipo de relación.
Consideraciones
El coeficiente de correlación de Pearson aumenta si aumenta la variabilidad de X y/o Y (las variables), y disminuye en el caso contrario. Por otro lado, para afirmar si un valor es alto o bajo, debemos comparar nuestros datos con otras investigaciones con las mismas variables y en circunstancias parecidas.
Para representar las relaciones de diferentes variables que combinan linealmente, podemos utilizar la llamada matriz de varianzas-covarianzas o la matriz de correlaciones; en la diagonal de la primera nos encontraremos con valores de la varianza, y en la de la segunda nos encontraremos con unos (la correlación de una variable consigo misma es perfecta, =1).
Coeficiente elevado al cuadrado
Cuando elevamos al cuadrado el coeficiente de correlación de Pearson, su significado cambia, e interpretamos su valor en relación a los pronósticos (indica causalidad de la relación). Es decir, en este caso, puede tener cuatro interpretaciones o significados:
1. Varianza asociada
Indica la proporción de la varianza de Y (una variable) asociada a la variación de X (la otra variable). Por lo tanto, sabremos que "1-coeficiente Pearson al cuadrado" = "proporción de la varianza de Y que no está asociada a la variación de X".
2. Diferencias individuales
Si multiplicamos el coeficiente de correlación de Pearson x100, nos estará indicando el % de las diferencias individuales en Y que están asociadas / dependen de / son explicadas por las variaciones o diferencias individuales en X. Por lo tanto, "1-coeficiente Pearson al cuadrado x 100" = % de las diferencias individuales en Y que no está asociado / depende de / es explicado por las variaciones o diferencias individuales en X.
3. Índice de reducción del error
El coeficiente de correlación de Pearson elevado al cuadrado también puede interpretarse como un índice de la reducción de error en los pronósticos; es decir, se trataría de la proporción del error cuadrático medio eliminado usando Y’ (la recta de regresión, elaborada a partir de los resultados) en vez de la media de Y como pronóstico. En este caso también se multiplicaría el coeficiente x 100 (indica el %).
Por lo tanto, "1-coeficiente Pearson al cuadrado" = error que se sigue cometiendo al usar la recta de regresión en vez de la media (siempre multiplicado x 100 = indica el %).
4. Índice de aproximación de los puntos
Finalmente, la última interpretación del coeficiente de correlación de Pearson elevado al cuadrado indicaría la aproximación de los puntos a la recta de regresión comentada. Cuando mayor sea el valor del coeficiente (más cercano a 1), más se aproximarán los puntos a Y’ (a la recta).
Referencias bibliográficas:
- Botella, J. Sueró, M. Ximénez, C. (2012). Análisis de datos en psicología I. Madrid: Pirámide.
- Lubin, P. Macià, A. Rubio de Lerma, P. (2005). Psicología matemática I y II. Madrid: UNED.
- Pardo, A. San Martín, R. (2006). Análisis de datos en psicología II. Madrid: Pirámide.
