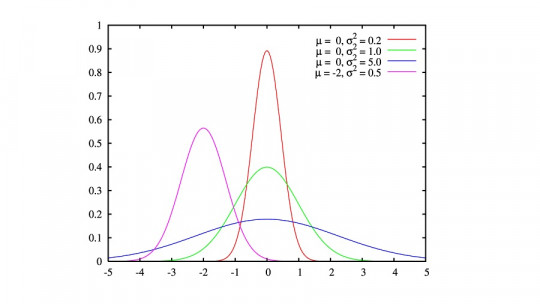
En estadística y probabilidad, la distribución normal, también llamada distribución de Gauss (en honor a Carl F. Gauss), distribución gaussiana o distribución de Laplace-Gauss, refleja cómo se distribuyen los datos en una población.
Se trata de la distribución más frecuente en estadística, y se considera la más importante por la gran cantidad de variables reales que adoptan su forma. Así, muchas de las características en la población se distribuyen según una distribución normal: la inteligencia, datos antropométricos en los seres humanos (por ejemplo la altura, la talla...), etc.
Veamos con más detalle qué es la distribución normal, y varios ejemplos de esta.
- Artículo relacionado: "Psicología y estadística: la importancia de las probabilidades en la ciencia de la conducta"
¿Qué es la distribución normal en estadística?
La distribución normal es un concepto perteneciente a la estadística. La estadística es la ciencia que se ocupa del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.
Una distribución describe cómo se distribuyen ciertas características (o datos) en una población. La distribución normal es el modelo continuo más importante en estadística, tanto por su aplicación directa (ya que muchas variables de interés general pueden describirse por dicho modelo), como por sus propiedades, que han permitido el desarrollo de numerosas técnicas de inferencia estadística.
La distribución normal se trata, pues, de una distribución de probabilidad de una variable continua. Las variables continuas son aquellas que pueden adoptar cualquier valor en el marco de un intervalo que ya está predeterminado. Entre dos de los valores, siempre puede existir otro valor intermedio, susceptible de ser tomado como valor por la variable continua. Un ejemplo de variable continua es el peso.
Históricamente, el nombre de “Normal” proviene del hecho de que durante un tiempo se creyó, por parte de médicos y biólogos, que todas las variables naturales de interés seguían este modelo.
- Quizás te interese: "Los 11 tipos de variables usados en investigación"
Características
Algunas de las características más representativas de la distribución normal son las siguientes:
1. Media y desviación típica
A la distribución normal le corresponde un media cero y una desviación típica o estándar de 1. La desviación típica o estándar indica la separación que existe entre un valor cualquiera de la muestra y la media.
2. Porcentajes
En una distribución normal, se puede determinar con exactitud qué porcentaje de los valores estará dentro de cualquier rango específico. Por ejemplo:
Alrededor del 95% de las observaciones está dentro de 2 desviaciones estándar de la media. El 95% de los valores se ubicará dentro de 1.96 desviaciones estándar con respecto a la media (entre −1.96 y +1.96).
Aproximadamente el 68% de las observaciones está dentro de una 1 desviación estándar de la media (-1 a +1), y alrededor del 99.7% de las observaciones estarían dentro de 3 desviaciones estándar con respecto a la media (-3 a +3).
Ejemplos de distribución gaussiana
Pongamos tres ejemplos para ilustrar, a efectos prácticos, qué es la distribución normal.
1. Estatura
Pensemos en la estatura de todas las mujeres españolas; dicha altura sigue una distribución normal. Es decir, la estatura de la mayoría de mujeres estará cerca de la estatura media. En este caso, la altura media española es de 163 centímetros en las mujeres.
Por otro lado, un número similar de mujeres serán un poco más altas y un poco más bajas que 163cm; sólo unas pocas serán mucho más altas o mucho más bajas.
2. Inteligencia
En el caso de la inteligencia, la distribución normal se cumple a nivel mundial, para todas las sociedades y culturas. Esto implica que la mayor parte de la población tiene una inteligencia media, y que en los extremos (por debajo, personas con discapacidad intelectual, y por arriba, superdotados), se encuentra menor parte de la población (el mismo % por debajo que por arriba, aproximadamente).
- Quizás te interese: "Las teorías de la inteligencia humana"
3. Curva de Maxwell
Otro ejemplo que ilustra la distribución normal es la curva de Maxwell. La curva de Maxwell, dentro del campo de la física, indica cuántas partículas de gas se mueven a una velocidad determinada.
Esta curva se eleva suavemente desde velocidades bajas, alcanza el pico en la media, y vuelve a descender suavemente hacia las velocidades altas. Así, esta distribución muestra que la mayoría de las partículas se mueven a una velocidad alrededor del promedio, característica propia de la distribución normal (concentrar la mayor parte de los casos en la media).
Referencias bibliográficas:
- Quintela, A. (2005). Estadística Básica Edulcorada. Bookdown.
- Fontes de Gracia, S. García, C. Quintanilla, L. et al. (2010). Fundamentos de investigación en psicología. Madrid: UNED. ISBN: 9788436260557.
- Botella, J. Sueró, M. Ximénez, C. (2012). Análisis de datos en psicología I. Madrid: Pirámide. ISBN: 9788436815382.
